« Je pense depuis un certain temps à faire ce que je propose dans ce billet. En bref, j’aimerais faire pour le ralentissement de la croissance en Europe le même exercice de comptabilité que j’ai fait pour les Etats-Unis dans mon livre Fully Grown. (…)
Pour les Etats-Unis, j’ai distingué entre un vingtième siècle marqué par une croissance relativement rapide et un vingt-et-unième siècle marqué par une faible croissance. Le PIB par tête aux Etats-Unis a augmenté à environ 2,25 % par an au vingtième siècle et à environ 1 % par an au vingt-et-unième siècle. Ce ralentissement semble s’être amorcé avant la crise financière mondiale, en l’occurrence à un certain instant autour de l’année 2000.
Est-ce la même chose pour l’Europe ? Fondamentalement, oui. (…) Commençons en regardant les Etats-Unis et la France. Dans le graphique ci-dessous, j’ai représenté le taux de croissance annualisé sur dix ans pour chaque année. Par exemple, en 2000, le graphique indique le taux de croissance entre 1990 et 2000. Les Etats-Unis ont connu une croissance juste supérieure à 2 % tout au long du vingtième siècle, avec un pic de croissance à la fin des années 1960 et au début des années 1970, mais ensuite le ralentissement s’amorce malgré la période 1998-2008. Il y a eu une accélération de la croissance en 2009-2019, en partie parce que le début de cette période correspond à la crise financière.
GRAPHIQUE 1 Taux de croissance sur 10 ans du PIB par tête des Etats-Unis et de la France (en %)
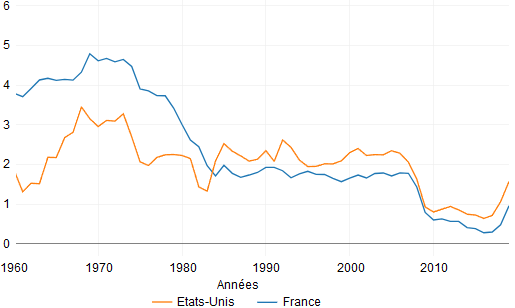
Et à propos de la France ? Les choses semblent légèrement différentes au cours des premières années. Entre 1960 et 1980, le taux de croissance a généralement été supérieur à celui des Etats-Unis, à environ 4 % par an. Et souvenez-vous qu’il s’agit de la croissance du PIB par tête, donc que le taux de croissance du PIB a été encore plus élevé. Après 1980, la France ressemble beaucoup aux Etats-Unis, avec une croissance d’environ 2 % jusqu’au début des années 2000 et, ensuite, elle a connu un ralentissement de la croissance dans des proportions similaires. (...)
Convergence versus ralentissement
Retournons à la France. Il y a deux ralentissements différents sur le graphique. Il y a le ralentissement entre 1970 et 1980, puis il y a le ralentissement entre 2000 et 2010. Comme dans mon livre Fully Grown, je ne m’intéresse qu’au second ralentissement. Le premier ralentissement est fondamentalement le mouvement de convergence de la France à son sentier de croissance équilibrée après la Seconde Guerre mondiale. Ce premier ralentissement de la croissance est, selon moi, presque entièrement explicable en termes de dynamique à la modèle de Solow. C’est une croissance de rattrapage, équivalente au fait de courir un peu plus vite que les autres pendant un petit moment parce que vous vous êtes arrêté pour refaire vos lacets. Une fois que vous avez rattrapé votre groupe, vous ralentissez naturellement jusqu'à vous caler à son rythme régulier.
Pour l’Europe en général, nous avons la même histoire. Le deuxième graphique est le même que le premier, mais avec des pays en plus. Le choix des pays est quelque peu arbitraire, mais en furetant dans les données je n’ai pas trouvé de différence substantielle. Il y a en général eu une période de croissance rapide au début (entre 1960 et 1980), reflétant la convergence, une croissance régulière à environ 2 % par an entre 1980 et 2000, et ensuite un ralentissement notable de la croissance. C’est sur ce dernier que ce billet porte. (…)
GRAPHIQUE 2 Taux de croissance sur 10 ans du PIB par tête des Etats-Unis et d'une sélection de pays européens (en %)
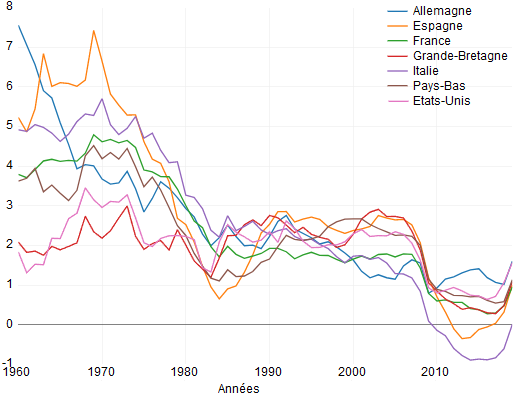
Si vous regardez le graphique, vous allez noter quelques différences par rapport à la France :
- Le Royaume-Uni n’a pas le même taux de croissance de rattrapage entre 1960 et 1980. Cela ressemble aux Etats-Unis, avec une croissance d’environ 2 % entre 1960 et 2000.
- L’Allemagne et l’Italie n’ont pas une période distincte de croissance régulière entre 1980 et 2000. Toutes les deux ont une croissance relativement élevée autour de 1960 et ensuite celle-ci décline continûment jusqu’au début des années 2000. L’Italie a une chute distincte dans son taux de croissance, similaire à la France, mais l’Allemagne ralentit moins vite. Mon hypothèse est que l’Allemagne et l’Italie ne sont fondamentalement pas différentes des autres, mais qu’elles n’ont juste pas eu le même ralentissement de la croissance à la fin du vingtième siècle.
- L’Espagne et les Pays-Bas ont eu des rebonds distincts autour de 1980 dans leurs taux de croissance, en croissant à un rythme élevé de 2,7-3 % par an pour l’essentiel des années 1990, avant le ralentissement du début des années 2000. A nouveau, je ne suppose pas que cela reflète un mécanisme vraiment différent, mais il va y avoir des différences intéressantes dans l’exercice de comptabilité.
Décomposons cela !
L’essentiel des pays d’Europe occidentale a connu un ralentissement de la croissance similaire à celui qu’ont connu les Etats-Unis à partir du début des années 2000. Comme je l’ai fait dans Fully Grown, je vais comptabiliser les sources de ce ralentissement de la croissance en distinguant les contributions suivantes : l’accumulation du capital physique, l’accumulation du capital humain et la croissance de la productivité.
Pour rafraichir votre mémoire, ce que j’ai trouvé dans Fully Grown à propos des Etats-Unis était que la grande majorité (pour ne pas dire la totalité) du ralentissement de la croissance pouvait être attribuée à une explosion de la croissance du capital humain au vingtième siècle comme les boomers entraient dans la population active et un frein sur la croissance du capital humain au vingt-et-unième siècle comme les boomers commencèrent à sortir de la population active. Une façon de voir l’expérience américaine est de dire que la croissance au vingtième siècle a été anormalement élevée parce que le taux d’emploi grimpa rapidement grâce aux boomers et que le ralentissement est une réaction naturelle à cette stimulation temporaire (…).
Concernant le capital humain, (…) plusieurs points me frappent. Premièrement, les Etats-Unis se singularisent. On retrouve le récit que j’en ai fait ci-dessus. Il y a eu une croissance relativement forte du capital humain au milieu du vingtième siècle (ajoutant environ 1,5-2 points de pourcentage à la croissance) et ensuite sa contribution est devenue négative au vingt-et-unième siècle, avec seulement une récente poussée (à nouveau, probablement un artefact de la crise financière). Aucun pays européen ne présente une telle évolution.
GRAPHIQUE 3 Taux de croissance sur 10 ans du capital humain des Etats-Unis et d'une sélection de pays européens (en %)
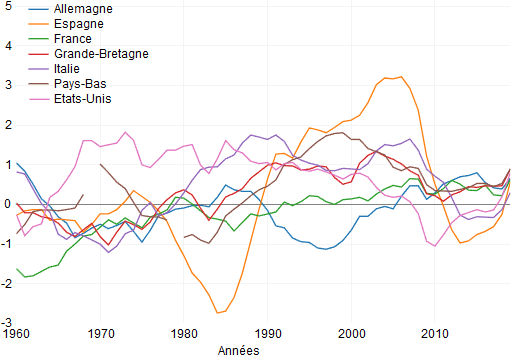
L’Allemagne a une croissance négative du capital humain tout au long du vingtième siècle, puis celle-ci est devenue positive autour de 2000, compensant le ralentissement de la croissance. La France a également eu une croissance négative du capital humain autour de 1960 et ensuite celle-ci est passée au-dessus de zéro. La situation du Royaume-Uni s’apparente à celle de l’Allemagne. Les Pays-Bas ont connu une croissance significative au capital humain lors des années 1990 et ensuite un lent déclin de celle-ci.
L’Italie a connu une explosion de sa croissance du capital humain à la fin du vingtième siècle et ensuite celle-ci est retombée au vingt-et-unième siècle. L’Espagne a conne une forte vague de croissance du capital humain à la fin du vingtième siècle qui a ensuite chuté au début du vingt-et-unième siècle, ce qui fournit au moins une partie de l’explication pour l’effondrement de la croissance espagnole. Ces deux dynamiques sont probablement les plus proches de celle observée aux Etats-Unis, mais l’échelle et le calendrier ne sont pas les mêmes. Aux Etats-Unis, vous pouvez voir un lent déclin de la croissance du capital humain avant 2000, ce qui est cohérent avec le vieillissement, tandis qu’en Italie et en Espagne la chute apparaît plus soudaine et le calendrier est tel qu’elle apparaît davantage comme une réponse à la crise financière mondiale qu’autre chose.
Enfin, que dire à propos de la croissance de la productivité ? Le graphique ci-dessous montre que, relativement aux Etats-Unis, un déclin de la croissance de la productivité est plus apparent pour l’Europe autour de l’instant du ralentissement de la croissance. Si vous regardez le cas des Etats-Unis, la croissance de la productivité augmente jusqu’à environ 2005 et ensuite elle diminue. Mais si vous regardez le Royaume-Uni ou la France, par exemple, leur croissance de la productivité reste à 2 % jusqu’à environ 2006 et ensuite elle chute à quasiment zéro, voire elle est parfois négative. C’est une chute de la croissance de la productivité bien plus forte que pour les Etats-Unis.
GRAPHIQUE 4 Taux de croissance sur 10 ans de la productivité des Etats-Unis et d'une sélection de pays européens (en %)
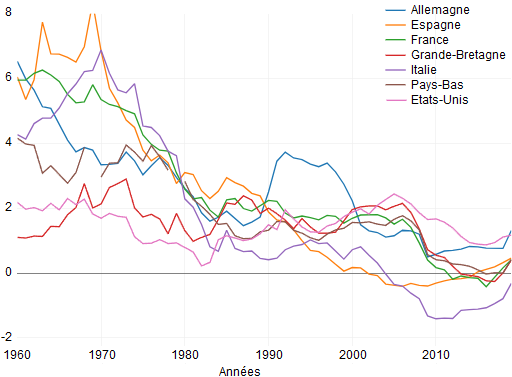
(…) Je tente quelques conclusions. Les changements dans l’accumulation du capital physique n’ont pas été importants pour le ralentissement de la croissance européenne. Les changements dans la croissance du capital humain ont été importants pour le ralentissement de la croissance européenne, mais cet effet varie d’un pays à l’autre. Cela ne nous dit pas si cela tient à la démographie (comme aux Etats-Unis) ou à d’autres facteurs du capital humain, comme les changements dans l’éducation ou le nombre d’heures travaillées. Une source significative du ralentissement de la croissance en Europe est due à une chute de la croissance de la productivité, assez généralisée. Cette chute a été plus forte qu’aux Etats-Unis. (...) »
Dietrich Vollrath, « Fully grown - European vacation! », Growth Economics blog, 29 décembre 2022. Traduit par Martin Anota
aller plus loin...
« Comment expliquer le ralentissement de la productivité dans les pays avancés ? »
« Comment le vieillissement démographique affecte-t-il la croissance de la productivité ? »
« Pourquoi la croissance de la productivité a-t-elle ralenti ? »
« L'essoufflement de la productivité, une pathologie transatlantique ? »
« La faible croissance de la productivité en Europe, un héritage de la crise financière ? »